“Queueing Theory in Practice: Performance Modeling for the Working Engineer” by Eben Freeman

Queueing Theory helps us understand our systems:

• approximate systems with models
• reason about behavior
• interpret data

Models:

• Are reductive, worthless without real data
  • Production or experimental data
• Allow data interpretation, predictions

Modeling Serial systems

System in question: Honeycomb ingestion API

• stateless, user-facing service
• higly concurrent, across many servers
• low latency target (<1ms-9ms)
• CPU bound

How to allocate appropriate resources for a service (e.g. on AWS) keeping costs minimal?

• Guesswork
• Production-scale load testing with generated traffic: expensive, time consumming
• Small experiments plus modeling: let’s do that

Small Experiment

Find the max request throughput for single-core (with a queue):

• generate requests arriving at an average throughput at random
  • [the ‘random’ part means a given request’s content is picked at random from a pool of possible request contents]
  • simulates independent clients
• measure latency at different throughput levels

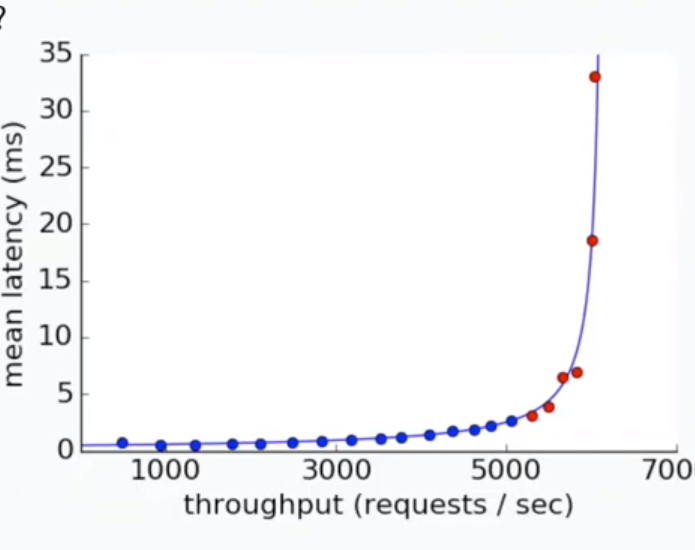
Experiment Data

Everything is smooth until it’s not:

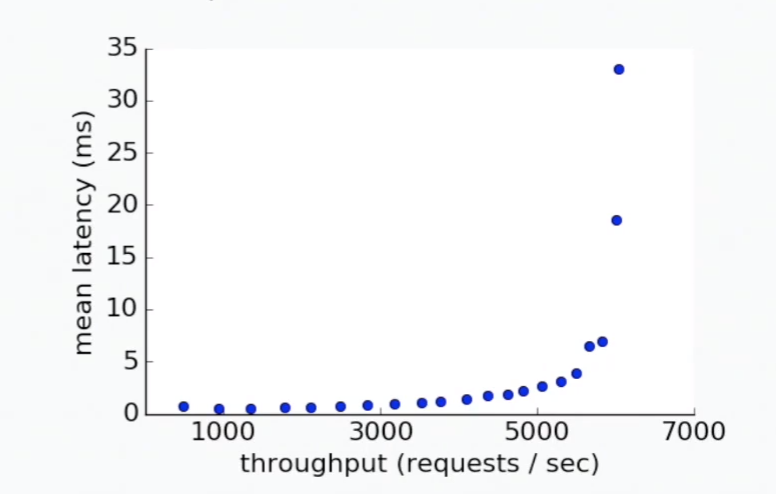
What’s the model that describes this?

Step 1: identify the question

• The busier the server, the longer tasks will wait in a queue
• As a function of throughput, how much longer does a task need to wait in the queue?

Step 2: identify the assumptions

• requests arrive independently
• requests are random
• requests arrive at an average throughput rate, but dont’ arrive at uniform constant times
• servicing one request takes a constant time
• we service one request at a time

Step 3: model the system
At 6:13, he shows that based on the assumptions, this describes the throughput vs wait time:

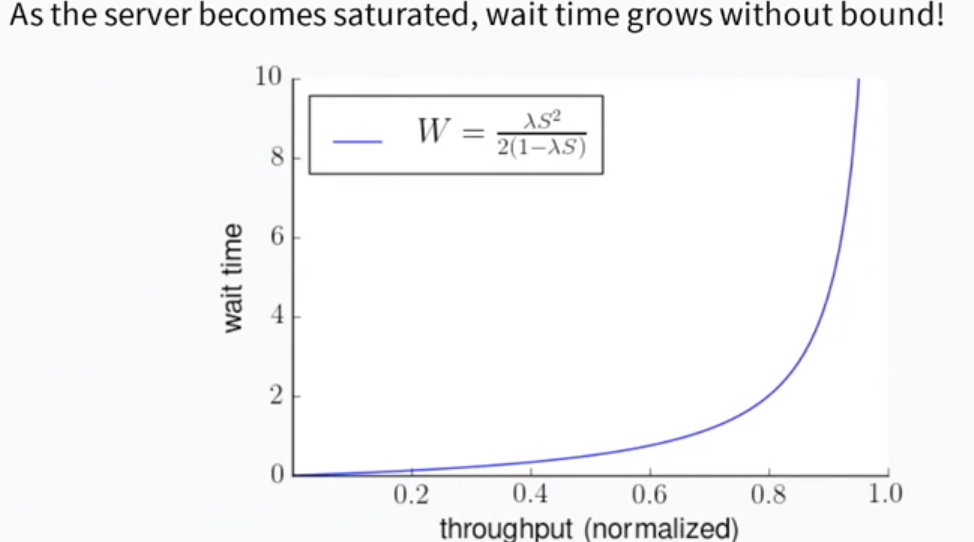
Model fits the curve well:

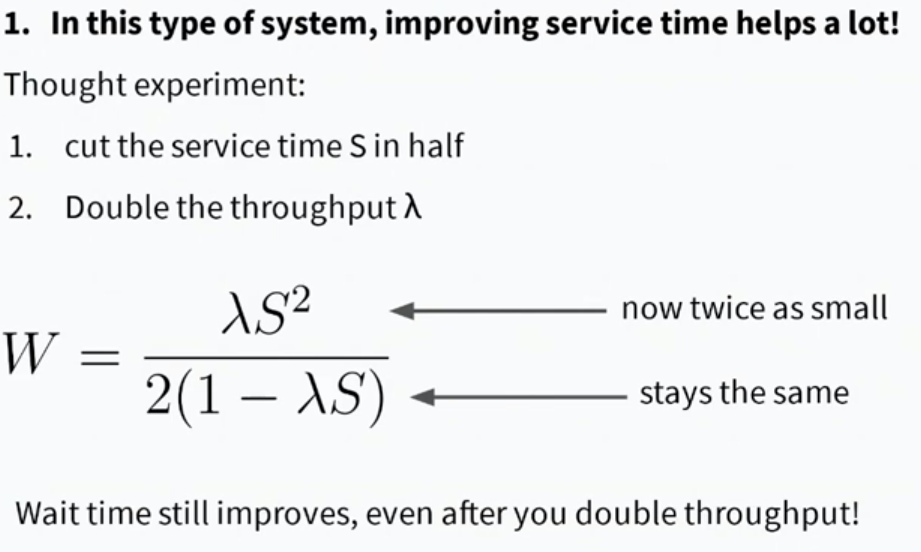
Improving service time has non-linear effects Model tells us halving service time and doubling throughput still results in a faster system. S is service time, lambda is throughput, W is wait:

Variability is bad
Variability in request arrival time and request processing time causes the queueing

• Requests arriving in bursts cause queueing
• Processing time that is different per request type causes queueing

What we can do:

• Batching
• Timeouts
• Client backpressure
• Concurrency control, limit concurrent requests

Modeling Parallel Systems

With multiple machines, we now need to decide: how to dispatch incoming requests

• e.g. round-robin, least busy server, randomly, etc.
• with optimal assignment e.g. least busy server and enough parallel machines, queueing problems appear to be solved

Optimal Assignemnt: Coordination is Expensive

Dispatching work requires a coordinators e.g. load-balancer

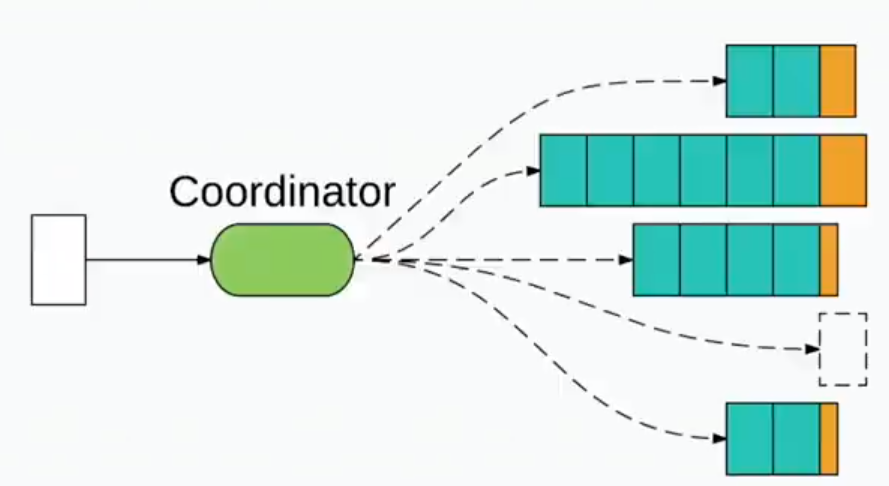
The coordinator needs to verify the load on each possible server

• so as to perform optimal assignment
• we have a coordination cost per request
• Universal Scalability Law kicks in: increasing parallelism carries a coordination cost proportion to the parallelism
  • given enough parallel systems, coordination is more expensive than the work performed
  • coordination degrades throuhgput at high parallelism

High Parallesim and Coordination

Paper to read: [The Power of Two Choices in Randomized Load Balancing] (https://www.eecs.harvard.edu/~michaelm/postscripts/tpds2001.pdf)
Systems to read about: Kraken, Scuba, Sparrow

Approximate Optimal Assignment
Instead of querying N servers for, query 2 randomly. Pick best of the pair.

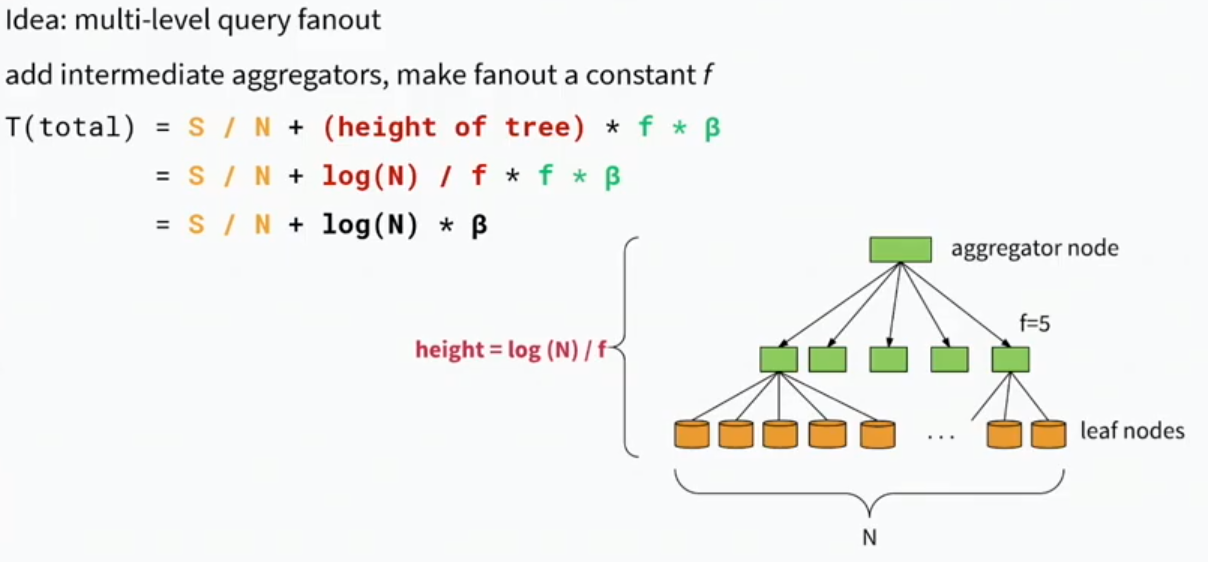
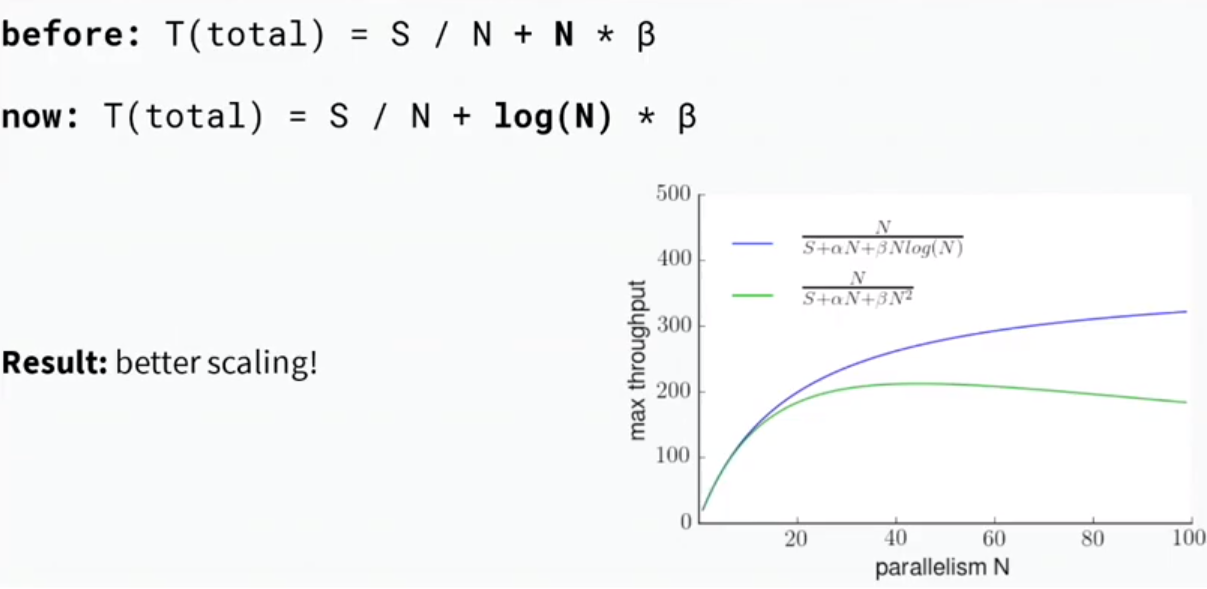
Iterative Partitioning

• We know throughput gets worse for large fan-out
• Use mulit-level fans-outs with intermediaries